Helpful links about Intonation:
Understanding Intonation
1. When did we start to learn about tuning?
|
Understanding Intonation: Perfect Intervals
Music has been part of human culture since the beginning of time. There have been many different instruments and many different types of tuning systems. Today different cultures use different types of tonal systems. There are a few things that are easily recognized in all of them. For example, the octave. Even someone who does not know much about music can recognize that the octave is a mirror image of the first note. The fifth is different but so closely related to the first note that it also is part of the first note. The fourth is the same as the fifth but upside down. So we must look at the seconds, thirds, sixths, and sevenths. These intervals do not fuse into one sound like the octave and fifth. They are more ambiguous. In fact, many of these intervals can be sharpened or flattened without changing the impression of the original interval. The slightest alteration of fourths, fifths, and octaves changes the interval completely.
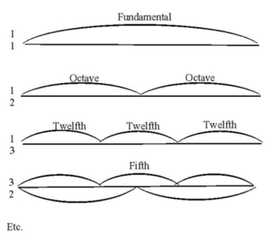
Understanding Intonation: Pythagoras For centuries, musicians have spoken of the problems of our tuning system. They have been perplexed and wondered, “How do we play in tune?” Consider long ago during Roman times. Pythagoras (570 B.C. to 495 B.C.), who discovered the numerical basis for acoustics, heard hammers being struck by a blacksmith. The crash of the hammers against anvils created different intervals. Using bells, Pythagoras constructed the overtone series. Then he used mathematics to represent the intervals. See chart below. |
Music to help your band navigate intonation better. |
Why do we no longer use some of these historical scales?
|
|
Understanding Intonation: Reproducing Intervals Using a monochord—a one-string sound board with a sliding bridge to produce pure tones—you can reproduce all of the following intervals with the proportions shown: Understanding Intonation: Pythagorean Scale
Theoretically, taking the mathematical ratio for 12 perfect fifths and adding them together should produce the same exact note as where we started, or at least the same note up 7 octaves. But we get: |
On the other hand, add the ratios of 7 octaves, and we get:
The octaves do not match. C8 overshoots the octave by about a quarter of a half step. This can create an excruciating octave to the ears which is so out of tune that it renders the note unusable. Pythagorean tuning also creates fast beating thirds, sixths, and smaller diatonic semitones, i.e. seconds and sevenths.
What if we try building scales on 5ths, 4ths, or 3rds?
Understanding Intonation: Constructing a scale with Major 3rds
The 5:4 ratio gives a lot of problems with equal temperament or even Pythagorean tuning. They leave the 5:4 interval or major 3rd very wide.
If we make 3rds so they are beatless, P5 (perfect 5ths) and P4 (perfect 4ths) are so out of tune they sound sour.
We get many of the same problems when we build a scale on 2nds except that equal temperament is based upon the minor 2nd. The octave is divided into 12 equal parts. This alters the P5 so it is 2 cents lower and P4 is 2 cents higher, but the octave is exactly in tune.
The 5:4 ratio gives a lot of problems with equal temperament or even Pythagorean tuning. They leave the 5:4 interval or major 3rd very wide.
If we make 3rds so they are beatless, P5 (perfect 5ths) and P4 (perfect 4ths) are so out of tune they sound sour.
We get many of the same problems when we build a scale on 2nds except that equal temperament is based upon the minor 2nd. The octave is divided into 12 equal parts. This alters the P5 so it is 2 cents lower and P4 is 2 cents higher, but the octave is exactly in tune.
Understanding Intonation: Constructing Scales with 5ths
How do we create a scale with the pure octave but not compromise the pure sounding fifths, fourths, or even thirds and sixths? The answer is you cannot, that is to say you cannot on a tempered instrument like the piano or organ. You must make one of two choices to make the instrument usable.
1. Alter the one fifth (F7 to C7) and create a very sour fifth—or, as it is called, “the wolf”--so it is in unison with the beginning note but out of tune with F7.
2. Alter all the fifths so that they are all a little smaller than pure (1/12th to be exact) so that the octaves still sound in tune.
Scales with 4ths
Can we construct a scale using different intervals? The 4:3 interval or fourth is an inverse of 3:2. So if you must shrink fifths to play octaves in tune, then you must expand fourths to play octaves in tune.
How do we create a scale with the pure octave but not compromise the pure sounding fifths, fourths, or even thirds and sixths? The answer is you cannot, that is to say you cannot on a tempered instrument like the piano or organ. You must make one of two choices to make the instrument usable.
1. Alter the one fifth (F7 to C7) and create a very sour fifth—or, as it is called, “the wolf”--so it is in unison with the beginning note but out of tune with F7.
2. Alter all the fifths so that they are all a little smaller than pure (1/12th to be exact) so that the octaves still sound in tune.
Scales with 4ths
Can we construct a scale using different intervals? The 4:3 interval or fourth is an inverse of 3:2. So if you must shrink fifths to play octaves in tune, then you must expand fourths to play octaves in tune.
Pythagorean Tuning vs. Equal Temperament?
Understanding Intonation: Comparing Temperaments
In equal temperament the 4:3 P4 and 3:2 P5 are only slightly out of tune, but the M3 and m3 are left extremely wide. Mathematically the 3rd is left about 1/7 of a note wider than a P4. This is better than the wolf (Pythagorean Tuning), which is 1/4 of a note off. Today we have even accepted this interval and many times do not even talk about it. Some musicians even claim to prefer the acoustically impure 3rds over pure sounding 3rds. This phenomenon comes from the fact that when you add two or three strings together on pianos, the intonation between intervals becomes hidden so that many people cannot hear the pitch problems. If you isolate the strings so only one string is ringing, the intonation is much clearer for everyone to hear.
Try this simple experiment: Play a major 10th on the piano, that is a 3rd plus an octave. It beats quite fast. As you ascend the piano keyboard, it should get faster and faster, and as you descend it should get slower because the temperament has been set to do that.
If you set up two Peterson Strobe Tuners to play an equal tempered C4 and E4, 400 cents higher or in mathematical terms 1.25992 ratio (corresponds to equal temperament), you will hear an unusually large amount of beats (out of tune). In Pythagorean system, E4 is 408 cents higher than equal temperament, giving even faster sounding 3rds.
In equal temperament the 4:3 P4 and 3:2 P5 are only slightly out of tune, but the M3 and m3 are left extremely wide. Mathematically the 3rd is left about 1/7 of a note wider than a P4. This is better than the wolf (Pythagorean Tuning), which is 1/4 of a note off. Today we have even accepted this interval and many times do not even talk about it. Some musicians even claim to prefer the acoustically impure 3rds over pure sounding 3rds. This phenomenon comes from the fact that when you add two or three strings together on pianos, the intonation between intervals becomes hidden so that many people cannot hear the pitch problems. If you isolate the strings so only one string is ringing, the intonation is much clearer for everyone to hear.
Try this simple experiment: Play a major 10th on the piano, that is a 3rd plus an octave. It beats quite fast. As you ascend the piano keyboard, it should get faster and faster, and as you descend it should get slower because the temperament has been set to do that.
If you set up two Peterson Strobe Tuners to play an equal tempered C4 and E4, 400 cents higher or in mathematical terms 1.25992 ratio (corresponds to equal temperament), you will hear an unusually large amount of beats (out of tune). In Pythagorean system, E4 is 408 cents higher than equal temperament, giving even faster sounding 3rds.
“What makes anyone think those are acceptable tunings?” Arthur Benade
Now lower the E4 (note E in 4th octave) from the ratio to the mathematical ratio 5/4, 1.25 or 384 cents higher. You can now hear a pure sounding third, this is why you are always asked to lower the major third.
C. P. E. Bach, describing a temperament, felt “most of the fifths” should be narrowed a very small amount so all keys would be usable.
“Temperaments are closed systems designed to help make the intonation of instruments with immovable pitch (like the organ and harpsichord) convincing. But singers and players of stringed and wind instruments have no such limitations. Temperament is too rigid a concept to apply to them.”
Now lower the E4 (note E in 4th octave) from the ratio to the mathematical ratio 5/4, 1.25 or 384 cents higher. You can now hear a pure sounding third, this is why you are always asked to lower the major third.
C. P. E. Bach, describing a temperament, felt “most of the fifths” should be narrowed a very small amount so all keys would be usable.
“Temperaments are closed systems designed to help make the intonation of instruments with immovable pitch (like the organ and harpsichord) convincing. But singers and players of stringed and wind instruments have no such limitations. Temperament is too rigid a concept to apply to them.”
Utility of Equal Temperament
Understanding Intonation: Utility
Equal temperament did several things to improve music. It made the manufacturing of instruments much easier by creating a standard tuning system for designing instruments and also made the possibility of advanced polyphony conceivable. Music since the Baroque Period has used a somewhat more tempered system because of its flexibility in all keys.
Equal temperament did several things to improve music. It made the manufacturing of instruments much easier by creating a standard tuning system for designing instruments and also made the possibility of advanced polyphony conceivable. Music since the Baroque Period has used a somewhat more tempered system because of its flexibility in all keys.
Paul Hindemith stated ”All composer’s nowadays make use of the extended harmonic and melodic relations that result from the use of an adequate theoretical foundation. They still try to cram every manifestation within the narrow confines of diatonic interpretation.”
Meaning, with all the extended chords and non-tonal music of today, it is too difficult to try and play with Just Intonation. With this, Hindemith is correct. Still, there is music that could be more beautiful with an adjustable tuning system.
Meaning, with all the extended chords and non-tonal music of today, it is too difficult to try and play with Just Intonation. With this, Hindemith is correct. Still, there is music that could be more beautiful with an adjustable tuning system.
Just Intonation
Understanding Intonation: Alternate Temperament Systems
Why do we even adjust notes within different keys when for hundreds of years we have been trying to come up with equal temperament? Just Intonation is more beautiful, and, in fact, we can find examples of how to adjust different notes by studying some of the greatest musicians and composers of all time.
Why do we even adjust notes within different keys when for hundreds of years we have been trying to come up with equal temperament? Just Intonation is more beautiful, and, in fact, we can find examples of how to adjust different notes by studying some of the greatest musicians and composers of all time.
Also, it is important to recognize that such enharmonic modulations, where they are genuine, do really mystify the listener, whether the instrument is a rigidly tempered affair like the pianoforte with all its distinctions ironed out into twelve semitones to the octave, or whether, like the human voice, the violin, and the slide-trombone, it makes its own intonation and can approach mathematical ideals to the limits of human muscular accuracy.
Thomas Attwood, who took lessons from Mozart at age 19, described different intervals that Mozart indicated within Attwood’s music as he studied with him, “mezzo tuono grande” (major semitone) and “mezzo tuono piccolo” (minor semitone) and it is clear that the diatonic semitone is large and the chromatic semitone is small. A semitone is a half-step.
Daniel Gottlob Turk, a theorist and teacher from the late 18th century and early 19th century, stated, “A whole tone (C-D) consists of 9 parts, a large semitone D-Eb, consists of five parts but a small semitone Eb to E only four, or four from D to D# and five from D# to E.”
We can see from these that notes are to be played differently depending on whether they are sharp or flat, flat notes being a little higher than sharp notes.
Haydn, in his music Op. 77, no. 2 in F, stipulated that “listesso tuono” or “the same note” between a Eb and a D# confirming the fact that normally he wanted those notes played differently but in this instance he wanted them to be the same.
Thomas Attwood, who took lessons from Mozart at age 19, described different intervals that Mozart indicated within Attwood’s music as he studied with him, “mezzo tuono grande” (major semitone) and “mezzo tuono piccolo” (minor semitone) and it is clear that the diatonic semitone is large and the chromatic semitone is small. A semitone is a half-step.
Daniel Gottlob Turk, a theorist and teacher from the late 18th century and early 19th century, stated, “A whole tone (C-D) consists of 9 parts, a large semitone D-Eb, consists of five parts but a small semitone Eb to E only four, or four from D to D# and five from D# to E.”
We can see from these that notes are to be played differently depending on whether they are sharp or flat, flat notes being a little higher than sharp notes.
Haydn, in his music Op. 77, no. 2 in F, stipulated that “listesso tuono” or “the same note” between a Eb and a D# confirming the fact that normally he wanted those notes played differently but in this instance he wanted them to be the same.
What do we need to change now we understand Just Intonation and how to make chords more beautiful?
Understanding Intonation: Applying What We Have Learned
There should be two different tuning systems used: one for fixed pitch instruments and one for adjustable instruments.
We must teach both systems if we want the music to sound in tune and more beautiful. This also means that chromatic tuners will not always work, but our ears will tell us when we are in tune. There must be unequal temperaments and major and minor semitones. It is less complicated for inexperienced players and younger musicians to just play in equal temperament, but it is more beautiful if we teach performers to use just intonation when possible.
What are some rules of pitch that can apply to this system?
There should be two different tuning systems used: one for fixed pitch instruments and one for adjustable instruments.
We must teach both systems if we want the music to sound in tune and more beautiful. This also means that chromatic tuners will not always work, but our ears will tell us when we are in tune. There must be unequal temperaments and major and minor semitones. It is less complicated for inexperienced players and younger musicians to just play in equal temperament, but it is more beautiful if we teach performers to use just intonation when possible.
What are some rules of pitch that can apply to this system?
- Non-fixed pitch instruments should “modify infinitely” the relationships between the notes of the scale whenever they are not playing with a fixed pitch instrument.
- Raise the leading tone when playing a solo and use lower leading tones when playing harmony.
- Sharps are a little fatter than flats, 1/9 of a note flatter to be exact, or in musical terms, there are nine commas (divisions) between a whole tone. A sharp raises the note 4 commas and a at lowers the note by 4 commas, making them one comma different from each other.
- When changing between enharmonic notes, do not change pitches. Generally you are changing tonality at these points, and it is better to leave them the same in this instance.
- Play 3rds more acoustically correct with no beats. To many this will sound wrong or be too far out of tune from what they are used to hearing, so try to lower major thirds and raise minor thirds.
- Play P5 a little higher when time permits so you can really play in tune.
- Play P4 a little lower than normal.
How do you teach Just Intonation to your band?
Understanding Intonation: Applying What We Have Learned
There should be two different tuning systems used: one for fixed pitch instruments and one for adjustable instruments.
We must teach both systems if we want the music to sound in tune and more beautiful. This also means that chromatic tuners will not always work, but our ears will tell us when we are in tune. There must be unequal temperaments and major and minor semitones. It is less complicated for inexperienced players and younger musicians to just play in equal temperament, but it is more beautiful if we teach performers to use just intonation when possible.
There should be two different tuning systems used: one for fixed pitch instruments and one for adjustable instruments.
We must teach both systems if we want the music to sound in tune and more beautiful. This also means that chromatic tuners will not always work, but our ears will tell us when we are in tune. There must be unequal temperaments and major and minor semitones. It is less complicated for inexperienced players and younger musicians to just play in equal temperament, but it is more beautiful if we teach performers to use just intonation when possible.
This is for physical copies of music shipped to you plus PDF of everything so you can make copies for your group if you do not have enough.
Band Intonation Exercises teach your band to listen and adjust the pitch. It shows the natural pitch tendencies of each instrument and gives ways to resolve pitch problems. Hints: and tips for each instrument. It includes MP3 practice tracks.
Each instrument gets a
- Pitch Tendency Chart
- Intonation Issues and Solutions
- 19 Pitch Tendency Exercises
- To practice and apply what you learn
Each Order Includes:
Paper copies for a regular-size band + Reproducible PDF (Sent Via email after)